Binary Arithmetic

Computers depend on arithmetic and numerical codes, and the simplest way to do arithmetic in an electronic computer is with base 2, the binary number system, so we start there....

place value - powers of 10, base 10 (recall anything to the 0 power is 1)
3072 = 3*10³ + 0*10² + 7*10¹ + 2*10⁰
This is easiest to write out from right to left, so you start counting powers from 0).  Note that we also need symbols for the numbers less than ten (0-9)
We think of 3072 as a number.  In this discussion that is too sloppy:  The symbolism is a numeral representing a number.
Another representation could be a pile of 3072 counters, or a Roman numeral MMMLXXII.  

Also we can make different numerals by using a different base, in particular the simplest one, and the one used in computers hardware:

Converting binary to decimal numerals

binary (base 2) use powers of 2 for place value and two symbols 0, 1, for the numbers less than 2:
I will use a subscript to indicate the different base:  11011₂ means the base 2 numeral 11011:  If we expand the powers explicitly from the right, in normal arithmetic, this means:
1*2⁴ + 1*2³ + 0*2² + 1*2¹ + 1*2⁰
= 16 + 8 + 2 + 1 = 27₁₀. 
The base 10 numeral 27 refers to the same number as the base 2 numeral 11011.

For base 2, where the only coefficients are 0 and 1, a shorthand for converting small base 2 numerals to decimal is to think of the sequence of the possible powers of 2, and then just add in the ones where there is a 1 in the base 2 numeral:

Binary to decimal conversion is done directly by Python.  Try the following in the Python Shell, stopping without a close parenthesis, and look at the popup window in the Python shell, pointing out possible parameters:
int('11011'
note the second optional parameter, the base.  Finish as
int('11011', 2)
see the correct answer.

Converting decimal to binary numerals

Now we go in the other direction:  finding the binary place values from a given integer number:
Suppose we have an unknown int, i, which can be represented as a 4 digit decimal.  How could we recover the digits by doing simple arithmetic?  (On a computer, there is really something to do here, since the number is actually stored in a binary form.)  A small amount of algebra can show us the general approach:  For the algebra we name the 4 digits, say p, q, r, s, then we have
i = p*10³ + q*10² + r*10¹ + s
Note all but the last term are divisible by 10, so
s = i % 10
We have s, so we can remove it from our power sequence with integer division by 10. Change i so
i = i//10 =  p*10² + q*10¹ + r
Now use the same trick to recover r!  
r = i % 10
Continue, let
i = i//10 = p*10¹ + q
q = i % 10
One more time, let
i = i//10 = p
p = i % 10
To illustrate the general algorithm we can go through one more step:  Let 
i = i//10 = 0 - - getting  a 0 result means we are done.

This can turn into a general algorithm in Python:

def decimal(i):
  """return a string of decimal digits representing 
  the nonnegative integer i."""
  if i == 0:
    return "0"
  numeral = ""
  while i != 0:
    digit = i % 10
    numeral = str(digit) + numeral # add next digit on the LEFT
    i = i//10
  return numeral

Conversion to binary:  same idea as for digits of unknown number, but generate base is 2, not 10:

def toBinary(i):
  """return a string of binary bits representing 
  the nonnegative integer i."""
  if i == 0:
    return "0"
  numeral = ""
  while i != 0:
    digit = i % 2
    numeral = str(digit) + numeral # add next digit on the LEFT
    i = i//2
  return numeral

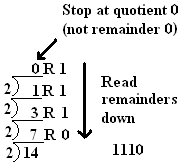
For illustration, this can also be done by hand.  To convert 14₁₀ to 1110₂, start with 14 (at the bottom of the picture) and repeatedly divide by 2 until you get a 0 quotient:
 

The conversion above from decimal  to base 2 and 10 using division and remainders are very similar, except for division by the right base. 

We get a numeral only if we have a separate character symbol for each of the numbers .    

For cryptography w will be interested in expansions in terms of a posibly large base g.  Buchmann refers to the g-adic expansion, giving all the coeficients for an
expansion in powers of g.  For cryptography we will often just use the representation of a list of integer coefficients, starting with the constant term.  If c is the list,
the number is the sum of all terms c[i]g**i.

Look at Python....

For some smaller bases it is convenient to have a numeral representation, with a single character for each possible coefficient,0, 1, .... g-1.  If g is no more than 10, obviously we use a subset of the standard decimal digits.  There is a standard extension for g = 11 through 36, using the usual digits and the first part of the alphabet: 
0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ. 
In particular base 16, hexadecimal is often used, with letter symbols through F for 15.

Hence the base 16 numeral 2A8C  can be expressed as a sum of terms for different powers of 16.  To express this in terms of normal base 10 numerals,  you have to also convert individual digits.  In particular hexadecimal A means decimal 10 and hexadecimal C means decimal 12. The full expansion, with powers increasing from the right, is

More Python....

See bases.py

Formatting Binary, Octal, and Hexadecimal in Python

You can generate hexadecimal, octal, and binary numerals in format strings in Python using format specifiers 'X', 'o', and 'b'  (letter o, for octal, not the number 0).  The base formatting may be used in the format function or after a colon inside braces in the string format method:

print 'binary:', format(27, 'b')
print 'decimal: {0}, hex: {0:X}, octal: {0:o}, binary: {0:b}'.format(27)

prints:  
binary: 11011
decimal: 27, hex: 1B, octal: 33, binary: 11011

Also Python recognizes binary, octal, and hexadecimal numeric literals.  The literals start with 0 followed by the specifiers b, o, or X, and then digits appropriate for the base.  Each of these literals is equal to 11 in decimal:  0b1011, 0o13, 0XB.

Size and Time Analysis