Assignment 6
Contents:
Overview
Topic: High-Level Programming
Related Reading: Ch. 8.1-8.3 of Dale/Lewis
as well as Lab 8 of Meyer
Due:
Internet Requirements
For this assignment, we will rely at times on the Palgo software
demonstrated in class. You will need to have an external Internet
connection to run this software.
NOTE: Use the palgo version on the web here, not the version
on
the CS that came with the lab book. The version on the web has a
number
of bugs fixed.
Practice Problems
Problems to be Submitted (20 points)
- (6 points)
For this problem, you can use Palgo to
do the
work for you if you'd like. Though on a test, you would certainly be
expected to do such a problem on your own, so please make sure that
you fully understand the answer. - What value or sequence of values
will be printed when running
the following segment of code?
val = 3
while val < 6
print(val)
val = val + 1
end
- What value or sequence of values will be printed when running
the following segment of code?
val = 11
while val >= 7
val = val -1
print(val)
end
- (4 points)
Modify the PlotPoint subroutine in the following Palgo
program, so that it only plots a point in the case that x>2*y.
define PlotPoint(x,y)
draw(x,y)
end
/* include, but do not change anything below this line */
color("red")
repeat 1000 times
PlotPoint(random(20),random(20))
wait(100)
end
- (5 points)
Modify the PlotPoint subroutine in the following Palgo
program, so that it always draws the point x,y, however chooses the
color based on the following rules:
define PlotPoint(x,y)
draw(x,y)
end
/* include, but do not change anything below this line */
color("red")
repeat 1000 times
PlotPoint(random(20),random(20))
wait(100)
end
A typical result of running such a program is the following.
Please
be careful in handling the boundaries between colors precisely.
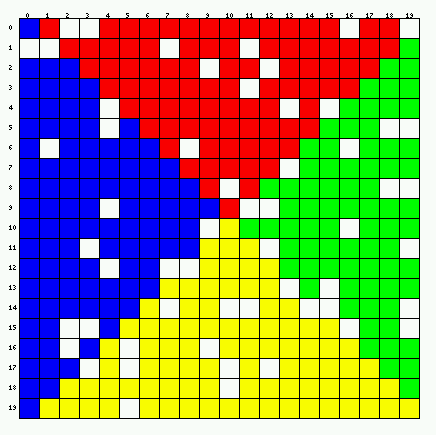
- (5 points)
Write a Palgo program which draws a red X across the entire grid, as
shown here:
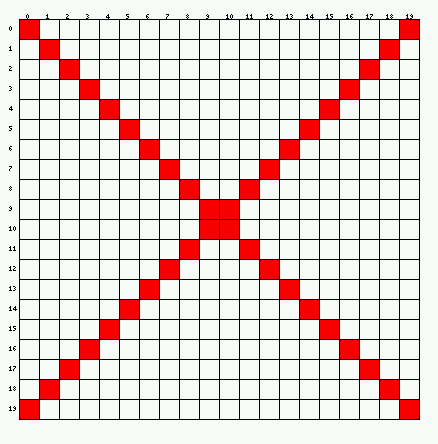
Overall, please type your answers to all of the problems in a single
document to be submitted electronically. Please see details about the submission process.
Extra Credit (2 points)
Write a subroutine
define rectangle(leftX,topY,width,height)
...
end
Which draws in a filled rectangle with the top left corner in
the given location and with specified dimensions.
Once you have tested this routine to see that it works, then you can
modify the "Random Colored Dots" program to develop a random colored
rectangles program, as described in the "Deeper Investigation" section
of Lab 8 of the Meyer text.
Two of many possible solutions for the subroutine in the last
practice problem follow. It is easy to make the height or width be off
by one.
Hopefully you corrected it if you saw that your original code
made a dimension one too big.
define L(x,y,h,w)
highY = y + h - 1
highX = x + w - 1
/* let corner be drawn by the second loop */
while y < highY
draw(x,y)
y = y+1
end
while x <= highX
draw(x,y)
x = x+1
end
end
define L(x,y,h,w)
goto(x,y)
down(h-1)
right(w)
end
Last modified: 1 October 2004

