
Binary is verbose! We will see that there is a very simple relationship between base 2 and base 16 = 24. Base 16 takes up about a quarter of the space of base 2, and so it is used in many places to communicate binary information compactly.
These notes are basically for everything except the Hands-on
Python Tutorial.
That is a free-standing unit that we take up after the Course
Introduction.
Videos for most of the sections below are in the beyondPython folder
in GoogleDocs, discussed in the Texts
section of the syllabus. Look there if you do not have the
videos.
Sections that correspond to the start of a video have (vid) at the end of the title.
Remember to do the introductory survey linked to the first day of class in the schedule.
Computer Science centers on algorithms:
unambiguous, step by step instructions for how to accomplish a
particular task in a finite amount of time.
Peter J. Denning lists seven main categories in computing
Computation (meaning and limits of computation)
Communication (reliable data transmission)
Coordination (cooperation among networked entities)
Recollection (storage and retrieval of information)
Automation (meaning and limits of automation)
Evaluation (performance prediction and capacity planning)
Design (building reliable software systems)
With all there many aspects, college introductions have handled things differently over time:
Historically students usually started with several heavy programming courses before anything else, giving little initial idea of all the other parts of computer science!
Then there was a reaction to breadth-first, essentially no programming. This is partly because in the past popular languages had a steep learning curve. Instead of much programming in a real computer language, breadth-first courses have brought algorithms written in English to a central place.
That brings us to the present with this course. Programming is important, and now there is an excellent recent language Python: extremely simple to learn and understand (close to English) and very powerful - why do much in English outlines when with about as much work you can run and demonstrate things on the computer using Python? Plus, even beginners can write programs to simplify their own personal tasks. Hence we spend a fair amount of our time on algorithms actually working with Python. We still keep the idea that Computer Science is much more than programming, and look at history, applications, and their relationship to the WWW. We dig down into the guts of a computer below what we see from the high-level language Python, to machine language and assembler code, and to the hardware underneath. We look beyond Python to application areas like graphics and web servers.
In an introductory course we cannot cover a whole lot with any depth, but we will deal at some level with all the areas: We will think about what we can compute. The last part of the section using Python will involve communication and cooperation between web client and server. We introduce a basic way to store information, in files. We will design, write and evaluate programs to automate the solution of problems.
For the programming in Python, we use custom tutorials written by me, Hands-on Python Tutorial. For the other areas, I have these online notes that you are reading. The home page lists many other references.
We are not alone in choosing Python: It is the language most being learned by professional developers. YouTube and DropBox are largerly written in Python. Python is the a popular language for applications using machine learning and big data analysis. Python is freely available for Windows, Macs, and Linux.
To get the projects:
I wrote the Hands-on Python Tutorial thinking specifially of Comp 150, though I leave it on the web for anyone to use, so it is not directly made into coursework on the web. Homework exercise links and topic timing are in the Course Schedule. Most, but not all, of the exercises in the Tutorial are included in the Comp 150 homework. Continue now in the Hands-on Python Tutorial.
The rest of these notes come in after you have finished with the Hands-on Python Tutorial.
We have seen how we can tell the computer what to do with the fairly simple syntax of Python. The course started there because it was relatively easy place to accomplish a lot. As you were introduced to it, Python was just given to you. We could immeditately see, experimenting in the Shell, that Python worked on your computer. But how? Python operates on the top of many layers of computer hardware and software. We are going to take an introductory exploration down into the hardware and logic of computers. Here is an outline of that path:
Binary arithmetic: We will see that everything in a computer gets encoded as a number. The hardware is built essentially on two state switches, that handle a bit of information at a time. We can use different names for the two choices: true and false or as 1 and 0. A compatible number system is important. Rather than our familiar decimal system, also call base 10, we will need to understand the binary system, also called base 2.Machine Language and Assembler: Next we work with the instructions that are part of the computer's hardware. To be feasible in hardware, the instructions need to be rather simple. They are the machine language of a particular computer. We will look at machine language (actually an extra simple model of a machine language), mostly though its more human friendly variant, assembler. We see how higher level ideas we express in languages like Python can be translated into, and implemented with, a very limited group of simple instructions. The Python interpreter does this conversion automatically for Python programs.
Boolean Logic and Circuits: Once we have an idea of how simple instructions can be combined to implement high level programs, the final stage is to look at how hardware can implement individual instructions. In Python we built up logical expressons with and, or, and not. We will look much more systematically at logical expressions, and see how they relate to circuits and machine language instructions.
Computers depend on arithmetic and numerical codes, and the
simplest way to do arithmetic in an electronic computer is with base
2, the binary number system. First review our usual decimal
system, in powers of 10:
place value
- powers of 10, base 10 (recall anything to the 0 power is 1)
3072
= 3*103 + 0*102 + 7*101 + 2*100
This
is easiest to write out from right to left, so you start counting
powers from 0). Note that we also need symbols for the numbers
less than ten (0-9)
We think of 3072 as a number. In
this discussion that is too sloppy: The symbolism is a numeral
representing a number.
Another representation could be a pile of
3072 counters, or a Roman numeral MMMLXXII.
Also we can
make different numerals by using a different base, in particular
the simplest one, and the one used in computers hardware:
(included in previous video)
Binary (base 2) uses powers of 2 for
place value and two symbols 0, 1, for the numbers less than 2:
I
will use a subscript to indicate the different base: 110112
means the base 2 numeral 11011: If we expand the powers
explicitly from the right, in normal arithmetic, this means:
1*24
+ 1*23 + 0*22 + 1*21 + 1*20
=
16 + 8 + 2 + 1 = 2710.
The base 10 numeral 27
refers to the same number as the base 2 numeral 11011.
For
base 2, where the only coefficients are 0 and 1, a shorthand for
converting small base 2 numerals to decimal is to think of the
sequence of the possible powers of 2, and then just add in the values
where there is a 1 in the base 2 numeral:
|
24 |
23 |
22 |
21 |
20 |
power notation |
|
16 |
8 |
4 |
2 |
1 |
decimal values of powers |
|
1 |
1 |
0 |
1 |
1 |
A sample base 2 numeral |
|
16 |
+8 |
+2 |
+1 |
= 2710 Sum of products (or sum powers with coefficient 1) |
Looking ahead, download pipFiles.zip,
and unzip it on your computer or on your flash drive. The
pipFiles directory also contains a module for
studying bases, bases.py. To follow along for now, open Idle in
this directory.
Binary to decimal conversion is done directly by Python.
Try the following in the Python Shell, stopping without a close
parenthesis, and look at the popup window in the Python shell,
pointing out possible parameters:
int('11011'
note the second
optional parameter, the base. Finish as
int('11011', 2)
see
the correct answer.
The
applet
http://courses.cs.vt.edu/~cs1104/number_conversion/convtop.html
illustrates
place values in all bases from 2 - 16, converted in either direction, with explanations.
Now we go in the other direction: finding the binary place
values from a given integer number:
Suppose we have an unknown
int, i, which can be represented as a 4 digit decimal. How
could we recover the digits by doing simple arithmetic? (On a
computer, there is something to do here, since the number is actually
stored in a binary form.) A small amount of algebra can show us
the general approach: For the algebra we name the 4
digits, say p, q, r, s, then we have
i = p*103
+ q*102 + r*101 + s
Note all but the last
term are divisible by 10, so
s = i % 10
We have s, so we
can remove it from our power sequence with integer division by 10.
Change i so
i = i//10 = p*102 + q*101
+ r
Now use the same trick to recover r!
r = i %
10
Continue, let
i = i//10 = p*101 + q
q = i
% 10
One more time, let
i = i//10 = p
p = i % 10
To
illustrate the general algorithm we can go through one more step:
Let
i = i//10 = 0 - - getting a 0
result means we are done.
This can turn into a general
algorithm in Python:
def decimal(i):
"""return a string of decimal digits representing
the nonnegative integer i."""
if i == 0:
return "0"
numeral = ""
while i != 0:
digit = i % 10
numeral = str(digit) + numeral # add next digit on the LEFT
i = i//10
return numeral
Decimal to binary conversion: same idea as for digits of unknown number, but generate base is 2, not 10:
def toBinary(i):
"""return a string of binary bits representing
the nonnegative integer i."""
if i == 0:
return "0"
numeral = ""
while i != 0:
digit = i % 2
numeral = str(digit) + numeral # add next digit on the LEFT
i = i//2
return numeral
For illustration, this can also be done
by hand. To convert
1410 to 11102, start with 14 (at the bottom of
the picture) and repeatedly divide by 2 until you get a 0
quotient:

Binary
is verbose! We will see that there is a very simple
relationship between base 2 and base 16 = 24.
Base 16 takes up about a quarter of the space of base 2, and so
it is used in many places to communicate binary information
compactly.
We have not discussed bases above 10 yet. Problem: We need 16 distinct one-character symbols for 0 through 15. You run out of symbols using normal digits at 9. Solution: then start with letters, so decimal 10 corresponds to hexadecimal A, 11->B, 12->C, 13->D, 14->E, 15->F. The following table for 0-15 decimal has columns for hexadecimal and also binary. We will find the binary useful shortly:
|
Dec |
Hex |
Bin |
|
0 |
0 |
0000 |
|
1 |
1 |
0001 |
|
2 |
2 |
0010 |
|
3 |
3 |
0011 |
|
4 |
4 |
0100 |
|
5 |
5 |
0101 |
|
6 |
6 |
0110 |
|
7 |
7 |
0111 |
|
8 |
8 |
1000 |
|
9 |
9 |
1001 |
|
10 |
A |
1010 |
|
11 |
B |
1011 |
|
12 |
C |
1100 |
|
13 |
D |
1101 |
|
14 |
E |
1110 |
|
15 |
F |
1111 |
The base 16 numeral 2A8C can be expressed as a sum of terms for different powers of 16. To express this in terms of normal base 10 numerals, you have to also convert individual digits. In particular hexadecimal A means decimal 10 and hexadecimal C means decimal 12. The full expansion, with powers increasing from the right, is
|
2 |
A |
8 |
C |
2A8C |
|
2*163 |
+ 10*162 |
+ 8*161 |
+ 12*160 |
= 10892 |
so using the explicit base subscripts, 2A8C16 =
1089210.
In Python the conversion of a number
0 through 15 to a hexadecimal digit character can be expressed many
ways. One clear approach is:
def digitChar(n):
'''return single character for digits with decimal value 0 through 15'''
if n < 10:
return str(n)
if n == 10:
return 'A'
if n == 11:
return 'B'
if n == 12:
return 'C'
if n == 13:
return 'D'
if n == 14:
return 'E'
if n == 15:
return 'F'
Notice that the digitChar function
trivially produces the right digit for any number 0, 1, 2, ...
9.
The conversion above from decimal to base 2
and 10 using division and remainders are very similar, except for
division by the right base. We can make a more general function
that will work with any base 2 through 16:
def intToBase(i, base):
"""Return a string representing the nonnegative integer i
in the specified base, from 2 to 16."""
i = int(i) # if i is a string, convert to int
if i == 0:
return '0'
numeral = ""
while i != 0:
digit = i % base
numeral = digitChar(digit) + numeral # add next digit on LEFT
i = i//base
return numeral
There is one further change in intToBase to accommodate bases from
11
through 16: Instead of creating a digit character with just
str(digit), digitChar(digit)is
needed, as defined above.
The intToBase function and
several others are include in bases.py
in pipFiles.zip file referenced
earlier. It sits in the examples directory for the course (not in
the Python tutorial
examples).
Understanding hexadecimal allows interpretation of colors in web pages or in Python graphics. The Python graphics module has the color_rgb function to generate custom colors based on values for the red, green and blue components in the range 0 to 255. Integers in this range can be described by a two place hexadecimal numeral. Look at what the color_rgb function actually produces in the Python Shell:
>>> from graphics
import color_rgb
>>> color_rgb(255, 35, 0)
'#ff2300'
After the marker '#' that indicates the color is not a predefined
color name, you see the hexadecimal for each color component, ff, 23,
and 00. The same system of '#' followed by six hexadecimal
characters is used in html source attributes, so you can see and
manipulate custom colors in html, too.
Now back to the easy conversions between binary and hexadecimal, mentioned earlier.
The basic idea is to convert each 4 bits of a binary numeral to a
single hexadecimal character. In detail:
Group the binary digits
in 4's, starting from the right. Example:
|
10111100 |
start |
|
|
1011 |
1100 |
split into groups of 4 bits, starting from the right |
|
8+2+1 |
8+4 |
convert: add powers where there is a 1 bit |
|
11 |
12 |
decimal results |
|
B |
C |
convert to hexadecimal digits |
|
BC |
final hexadecimal answer |
|
A bigger example:
|
1011110011 |
= 001001110011 but NOT 100111001100 |
||
|
10 |
1111 |
0011 |
split into groups of 4 bits, starting from the right |
|
2 |
8+4+2+1 |
2+1 |
convert groups of bits from binary |
|
2 |
15 |
3 |
decimal results |
|
2 |
F |
3 |
convert 2-digit results to hexadecimal digits |
|
2F3 |
final hexadecimal answer |
||
Now the reverse process:
|
2F3 |
starting hexadecimal numeral |
||
|
2 |
F |
3 |
hex digits |
|
2 |
15 |
3 |
decimal (skip if using table directly) |
|
0010 |
1111 |
0011 |
binary, padded to 4 bits |
|
001011110011 |
combined |
||
|
1011110011 |
final binary numeral, leading 0's stripped |
||
See bases.py
in the examples directory for the course. The hexToBin and
binToHex functions manipulate pieces of strings and use some of the
string methods and string indexing syntax from Chapter 2 of the
Hands-on Python Tutorial.
If you do not want to do any
arithmetic in converting between binary and hexadecimal, you can use
the decimal/hex/binary table above or run the table() function
in bases.py to produce:
Dec Hex Bin
0 0 0000
1 1 0001
2 2 0010
3 3 0011
4 4 0100
5 5 0101
6 6 0110
7 7 0111
8 8 1000
9 9 1001
10 A 1010
11 B 1011
12 C 1100
13 D 1101
14 E 1110
15 F 1111
Instant converter applets at
http://www.easycalculation.com/hex-converter.php
The
same idea works for conversion between binary and base 8, octal.
Octal is used to express some Unix/Linux 3-bit permission
codes.
(Optional) This section relates recent ideas to previous Python work, but it is not central to the current ideas. It is useful for testing simple results you work on by hand, like those in the next section.
You can generate hexadecimal, octal, and binary numerals in format
strings in Python using format specifiers 'X', 'o', and 'b'
(letter o, for octal, not the number 0). Like the syntax for
float formatting, the base formatting may be used in the format
function or after a colon inside braces in the string format
method:
>>> 'binary:', format(27,
'b')
'binary:
11011'
>>> 'decimal: {0}, hex: {0:X}, octal:
{0:o}, binary:
{0:b}'.format(27)
'decimal: 27, hex: 1B, octal:
33, binary: 11011'
Also
Python recognizes binary, octal, and hexadecimal numeric literals.
The literals start with 0 followed by the specifiers b, o (letter
o), or
X, and then digits appropriate for the base.
>>> 0b11011
27
>>> 0X1B
27
The built-in functions hex, oct, and bin generate strings with these
notations:
>>> bin(27)
'0b11011'
>>> hex(27)
'0x1b'
Conversions to do by hand
to check understanding: (You can confirm with Python.)
As the beginning of the Hands-on Tutorial indicated, computer hardward does not execute Python directly. Python and other high level langages must be converted to the very simple set of instructions that are directly built into the computer hardware, the machine language. This is the first place we look underneath high level languages.
As we will see more in the gates unit, the state inside a computer is usually electrical, and the most dependable system uses voltages, either high or 0 (grounded) . This means two possibilities. This is a bit of information, the smallest possible amount. We will arbitrarily refer to the two states as 0 and 1. This is convenient for the binary number system!
Computers have a Central Processing Unit (CPU) connected by wires to a memory unit. Operations take place inside the CPU, with some data maybe transfered in from memory or sent back to memory (and also external devices, though we will skip that part in our simple model).
Like in a Python string or list, memory is referenced by integer locations, 0, 1, 2, .... There are several design decisions: one is how much data to put in a single memory cell that can be individually referenced. A common unit is a byte = 8 bits. Pip uses a byte, as do the common processors used in Windows machines (and the latest Macs). While a bit has two possible states, a byte has 28 = 256 states. Another choice is how big to allow memory to be. So that one byte can used to refer to any cell in the memory or our simulated machine, we will assume memory consists of no more than 256 cells (a very limited machine!).
A concept encouraged by Von Neumann in the 1940's was to encode the instructions as a form of data in the computer. Before this approach, changing the program in a computer involved physically rewiring the computer! With Von Neumann's approach, an instruction would be represented as a number in the computer's memory. Hence an instructionmust be a sequence of 0's and 1's, like
00010100 00000100
I introduce the space in the middle only to delineate individual bytes.
Since accessing memory is slower than internal operations in the CPU, all CPU's have places for special data to be stored inside of them. One is an Instruction Pointer (IP), saying where in memory the next instruction starts. CPU's also have one or more fast temporary data storage locations, called registers. I follow the simple example in a text we used to use, the Analytical Engine, which has a single such location, called the Accumulator or Acc for short, that holds a byte of information, just like a memory cell.
For a simple conceptual view, look at the Pip Assembler simulator
in the class web examples. All files are included in
pipFiles.zip.
The zip archive contains the files needed for the
Pip Assembler Simulator: pipGUI.py, pipText.py, pip.py,
pipHelp.py, hexBin.py, and sample program files,
simple.bin, simple.asm, arith.asm, sum2n.asm, ifElse.asm....
The main program is pipGUI.py. Run it from the operating
system. In Windows that generally just involves double clicking
on it the file window. (No
need to be in Idle - you will not be messing with the
code.)
You
will see a graphical Window. Click on the purple button that says
BINARY, to see its 'native' state. Look at the window as its
various parts are described:
The state of the simulated computer is shown in the CPU (lower left) with its accumulator (Acc) and Instruction Pointer (IP). The middle blue and right yellow blocks display memory.
First focus on the big middle blue rectangle labeled CODE. Instruction code in Pip is placed at the beginning of memory. Each instruction takes up two bytes, so for convenience bytes are shown in pairs down the right portion of the main blue rectangle. We will need to keep track of the locations of these instructions, so the left column in the blue rectangle shows the address (in decimal) of the beginning of each instruction. Beside the decimal address label is the same address in binary. Because each instruction is two bytes, the address labels advance by 2's.
Now look at the right yellow rectangle labeled DATA. For simplicity of display, we arbitrarily assume that the data for program variables is stored in the second half of memory, starting at address 128. Each individual byte is a separate piece of data, so we show only one per line, at the right. For our simple programs we will never need more than 8 variables, so only eight locations are displayed. As in the code section, address labels in decimal and binary are shown.
The remaining parts of the display are for controlling the simulator. They do not correspond to parts of Pip. The left column of buttons and text boxes is labeled COMMANDS. You should have already clicked on the command button labeled BINARY.
Let us load a machine language program into Pip. Make sure you have downloaded simple.bin, in the same folder as the program pipGUI.py that you opened. You can open it in the Idle editor, to see the file format, if you like. It contains five binary instructions.
Type simple.bin into the Filename text box.
Warning: I saw an intermitent weird bug in Idle or the graphics package when
I tried to enter a filename: no text cursor and no response to
typing. I found if I clicked in a different window on my sceeen,
and then tried again, it worked. It could also happn with any
other text entry box, but only the first time. This warning is
now, inelegantly, displayed in the simulator window.
Once you have entered the file name, click LOAD. The contents of the file appear as the first five instructions in Pip.
All Pip instructions use the Accumulator. It is always a source of data and/or the destination of a result. There are two other ways Pip refers to data. One is to have the actual data encoded as the second byte of the instruction. The more common way is to refer to a location in memory. In this case the second byte is interpreted as the address in memory where the data resides. That explains the second byte, so now the first byte. It can be logically split into two four bit fields, for example
0001 0100 00000100
In Pip we will have fewer than 16 basic operations, which are encoded in the second four bits.
0001 0100 00000100
The 0100 of this example means load a value into the accumulator. We must distinguish where to get the value from, either the second byte of the instruction or a specified address in memory. The first 4 bits (actually only 1 bit is needed) determine this. The encoding is that 0000 means a memory address and 0001 means the actual data is in the second byte of the instruction. That latter is the case above, where the second byte is 00000100 or 4 in decimal, so the full meaning of the instruction is load the value in the second byte (4) into the accumulator.
Look at the Simulator screen. See that the accumulator (ACC) has a value of 0. The instruction pointer (IP) shows the next instruction to execute. It is also 0. If you look at address 0 in the simulator you see the instruction we have been discussing. Also note that the binary version of the address 0 in the code it highlighted in orange. To more easily follow what is going on, it will always match IP. Click STEP. IP and the corresponding highlight should advance to 2, and the value in the accumulator should become 00000100 (or 4 in decimal).
One more machine language instruction, the one at address 2:
00000101 10000000
or to look at the parts:
0000 0101 10000000
The second four bits 0101 determine the type of instruction. In this case it is "store the contents of the accumulator to an address in memory". The second byte gives the address 10000000 (or 128 decimal). For the Store instruction the second byte only makes sense as an address in memory, and the first four bits of the instruction, 0000, reflect this. Hence the full instruction says to store the accumulator value at memory location 128.
Click STEP again. Look at memory location 128 (or 10000000 in binary). Also note IP in the CPU.
We could continue, but this gets tedious. Reading this binary is a pain. One of the first programs people wrote was an assembler, which translates something a bit more human readable into this binary code. In the assember written for this machine, the first two instructions discussed could be written
LOD #4
STO 128
Still not English or as close as Python but closer! In place of the second four bit pattern we have a three letter mnemonic. LOD is close to LOAD. STO is the beginning of STORE. The pound sign is sometimes used to mean 'number'. The first instruction says to load the number 4. The second instruction does not have the '#'. This means the other interpretation of the second byte is used: it refers to a memory location. Be mindful of the presence or absence of '#'! It is easy to make a mistake.
Click the button NONE under commands. Now you see the instructions stated in assembler and all the address labels in decimal.
We will come back to machine language briefly at the end of our discussion of this simple CPU, but for the most part we will code things in assembler.
The next instruction is LOD #3. From the earlier examples you should be able to figure out what that does. Click STEP to check. The next instruction is ADD 128. It should be no surprise that this involves addition, and from the format you should see that it involves memory location 128. We need two things to add. Memory location 128 is one obvious operand. The accumulator is also available. So the instruction adds the accumulator and memory location 128. The final issue is where to put the result. Fancier CPU's than Pip have more options, but in Pip all results go to the accumulator, except in the STOre instruction where a value is copied FROM the accumulator. Hence the sum of the accumulator and memory location 128 are stored back into the accumulator.
Click STEP to check.
You can put the result of an addition or any other operation into memory: It just takes an extra step. Guess what the next instruction STO 129 does. Click STEP and check.
Next is the HLT instruction, short for HALT. Click STEP and
the program stops (indicated on the screen by '- -' as the instruction
pointer.
Click INIT. This resets IP and ACC to 0. You could step through the program again, or to see the result, just click RUN, and it goes (up to 100 steps) to the end.
In Python and other higher level languages we also store data in
memory. We refer to the data by name,
not number.
Using names is easier. The assembler can also handle
that. Click the button DATA under labels. Every place we had
address 128 before, we now have W, and every place we had address
129, we now have X. In this case the machine code was
disassembled (from machine code to assembler code). The machine
code did not include names, so the simulator fakes it, and always
uses the names you see in the DATA section labels, W, X, Y, Z, T1-4.
(These names have no particular significance: they
are the names used by the old Analytical Engine.) If
you load a file with variable names, including ones different than W,
X, ..., then pipGUI remembers them and uses them instead. (The
only restriction for the display is that they cannot be more than 8
characters long.) In Python, variable names always are linked to
data in memory. In the Pip Assembler Simulator, the relationship
is very simple and graphic!
Click HELP. See the message at the bottom. This gives context sensitive help. First click on HELP again for a summary. This shows all the help for the simulator operations. Return to here if you have questions. It covers the command buttons, the comment area at the bottom, the close button, and it mentions how to get an assembler summary:
Click the HELP button and then click in the blue CODE area. Try that now. For reference, the contents of this window are shown below:
Pip Assembler Summary
Symbols Used
X for a symbolic or numeric data address.
#N for a literal number N as data
Acc refers to the accumulator
L refers to a symbolic code label or numeric code address
Instructions Pseudo Python syntax for what happens
Data Flow
LOD X (or #N) Acc = X (or N)
STO X X = Acc (copy Acc to location X)
Control
JMP L IP = L (go to instruction L)
JMZ L if Acc==0: IP = L else: IP = IP+2 (normal)
NOP No operation; just go to next instruction
HLT Halt execution
Arithmetic-Logic
ADD X (or #N) Acc = Acc + X (or N)
SUB X (or #N) Acc = Acc - X (or N)
MUL X (or #N) Acc = Acc * X (or N)
DIV X (or #N) Acc = Acc / X (or N)
AND X (or #N) if Acc != 0 and X != 0: Acc=1 else: Acc=0
NOT if Acc == 0: Acc = 1 else: Acc = 0
CPZ X if X == 0: Acc = 1 else: Acc = 0
CPL X if X < 0: Acc = 1 else: Acc = 0
In source files: An instruction may be preceded by a label
and a colon. Any line may end with a comment. A comment
starts with ';' and extend to the end of the line.
We will gradually introduce most of the 14 instructions and the assembler syntax conventions.
See arith.asm from the pipFiles:
LOD #7 ; acc = 7
initialize variables
STO W ; W = acc
LOD #3 ; acc = 3
STO X ; X = acc
LOD #6 ; acc = 8
STO Y ; Y = acc
; Z = (W + X) * Y / 2
LOD W ; acc = W
ADD X ; acc = acc + X ( = W+X )
MUL Y ;
acc = acc * Y ( = (W+X)*Y )
DIV #2 ; acc = acc/2 ( = (W+X)*Y/2
)
STO Z ; Z = acc
( = (W+X)*Y/2 )
HLT
Human comments are allowed starting with a ';' (same idea as the '#' in Python, but # is already used in Pip assembler.) In the example the comments are a very direct translation into pseudo Python. I use symbolic data names.
Load arith.asm into pipGUI by typing in the name under filename, and clicking LOAD. You should see the code, minus comments.
If you switch your view to the text console (what would appear in
the Python Shell in Idle) at any point, you will see that
the computer is showing you the results of playing computer: A
full history is kept. (I will expect you to show your
understand sequences of Pip instructions by playing computer, and
this text history shows you exactly what you should be able to
generate! You can write your own examples and test
yourself.)
When the program has halted, press INIT to
reinitialize the CPU. By hand edit some of the LOD instructions
that initialize the values of W, X, and Y. You could STEP through
to see one
line at a time execute. If you merely want to see the final
result, just press RUN, and the program runs up to 100 steps or until
it halts. If you look at the text window, you see the whole
history.
Consider two ways to sum from 1 to n in Python:
sum = 0
i = 1
while i <= n:
sum = sum + i
i = i+1
In assembler it is easier to sum from n down to 1, so the test is a comparison to 0:
sum = 0
while n != 0:
sum = sum + n
n = n-1
For a loop you need to change the order of execution. There is not a WHILE in Pip assembler: There are only the low level instructions JMP and JMZ. The essence of this section is seeing how to use JMP and JMZ to accomplish the same things as Python's while and if-else statements.
For example
JMP 12
means jump to the
instruction at address 12. in other words, set IP to 12,
rather than advancing IP by 2, like usual.
JMZ (Jump if zero) is a conditional
jump. For example
JMZ 20
means jump to
address 20 if the accumulator is zero. Otherwise go on
to the next instruction normally. In Pythonesque pseudo code:
if acc == 0:
IP = 20
else:
IP = IP + 2 # the usual
case
Both these instructions are needed to translate the Python while loops above: This is the first time in the assembler examples that the exact instruction locations are important, so I show the addresses on the left. My assembler allows you to enter optional numeric address labels followed by a colon before any instruction (as long as you give the memory address accurately):
0: LOD #4 ;
n = 4 # high level for
comparison
2:
STO
n
4:
LOD #0 ; sum =
0
6:
STO
sum
8:
LOD n ; while n != 0:
10:
JMZ 24
12:
ADD sum ; sum = sum +
n
14:
STO
sum
16:
LOD n ; n =
n - 1
18:
SUB
#1
20:
STO
n
22:
JMP 8
24:
LOD sum ; # for easy display - result in
accumulator
26:
HLT
As with the data addresses considered earlier, we are writing numerical addresses rather than meaningful names. This is also particularly awkward if you insert a new instruction and change a bunch of addresses. An better alternative is symbolic address labels. The previous code with numerical addresses for jumps above is slightly modified below to have symbolic code address labels. The code is sum2n.asm in pipFiles:
LOD
#4 ;
n = 4 # high level for
comparison
STO
n
LOD #0 ; sum =
0
STO
sum
LOOP: LOD n ;
while n != 0:
JMZ DONE
ADD sum ; sum = sum +
n
STO
sum
LOD n ; n =
n - 1
SUB
#1
STO
n
JMP LOOP
DONE: LOD sum ; # for easy display - result in
accumulator
HLT
PipGUI allows symbolic names up to 8 characters long, followed by a colon, to be placed before an instruction that is a jump target, and then the same name can be used in the JMP or JMZ instruction. In the code above LOOP is both an instruction label and the target in the JMP instruction. DONE is both a label and the target in the JMZ instruction. The while loop syntax is certainly clearer, but it is an easily automated step in a compiler to switch to the low-level version, so you do not have to worry about it in a Python program! Unlike with Python, the indentation I show for sum2n.asm is not significant to the assembler. It is merely my convention for easy reading by humans.
If you want to see numeric code addresses in the simulator, you
can press the DATA button under LABELS to see only data labels, but
not the code labels that I (and all real assemblers) allow. In
that view you see the LOD n instruction
is at address 8, and the JMP instruction has operand 8. Similarly
DONE is replaced with 24 in both places it appeared. The
assembler is smart enough to
count statements to determine correct addresses and to use those
numbers
to translate symbolic address labels.
Next step through the program and make sure everything makes sense. The new features here are the jumps. I WILL ask you to play computer on paper on a test to follow such a program. With the simulator, you can check yourself by following as you single step or by looking at the history that pipGui records in the text window. After running sum2n.asm, here is the log:
------ CPU initialized from sum2n.asm ---------1. Absolute value, in Python: x = abs(x)
Without the function call we could use the code
if
x < 0: # if x<0, do the next line; otherwise skip
the next line
x = -x
....
You want to skip the assignment if the condition is false, so a conditional jump is involved, but you do not to jump back to the heading at the end, as in a loop. This is the first time we have dealt with an inequality. Look at the instruction summary. There is just one instruction that deals with an inequality....
See if you can work this out. The solution is example abs.asm,
and it is worked out in the video.
2.
Another example: Redo sum2n.asm where you actually translate
while n >= 0:
directly
( not the condition used implicitly before, n
!= 0). Look at the full Pip assembler instruction set.
Note that there is only one instruction that deals with
inequalities, so you have to figure out some way to make it
work. The additional problem here is that you could test n < 0,
directly, but you want the opposite result. If you want the
opposite boolean result with Python, what is the word you use?
Look in the Pip instruction set: you will see the same word as the
instruction mnemonic! Whereas in Python you can put several
operations in the same instruction, recall that in assembler you can
only do one at a time.... A solution is shown in example as
sum2na.asm. It is only the treatment of the condition that is
changed from sum2n.asm.
Use
the simulator to test a version that you write or use example
sum2na.asm. Be sure you do this for yourself, or at least follow the
solution in sum2na.asm! You will need this idea later.
3. If-else statements are more involved. Let's start with a translation of
if x != 0:
y = 2
else:
y = 3
x = 5
For simple testing, let us set x in memory in the simulator before
running. That way we do not need to start by storing a value for
x. (Each of the other examples in this section will deal with
variable initialization similarly.)
We have evaluated conditions.
Testing if x != 0 just involves loading it and a JMZ to somewhere.
LOD x ; if
x!=0
JMZ ____
We have worked out the approach to assignment statements. Let us suppose the statements in the assember code follow the textual order of the Python. I'll put those sections with space between them for further editing:
LOD
x ; if x != 0
JMZ ____
LOD #2 ;
y=2 if-true clause
STO y
LOD #3 ;
y=3 if-false clause
STO y
LOD #5 ;
x=5 past if-else statement
STO x
The flow of control is new here. We will need jumps inserted. If the condition is true, we just fall into the if-true block, but if it is false we must get to the else part, which will require a label as a jump target. An easy name would be ELSE. It goes as the operand of JMZ and a label on the if-false part:
LOD
x ; if x != 0
JMZ ELSE
LOD #2 ;
y=2 if-true clause
STO y
ELSE: LOD #3 ; y=3 if-false clause
STO y
LOD #5 ;
x=5 past if-else statement
STO x
Also note that if the condition is true, Python would do the if-true
block and automatically skip the else
part each time. In assembler we have to be explicit. That will
require a jump from the end of the if-true block that happens every
time that block is run (JMP, not JMZ), requiring another jump target past the end of the
if-else statement. Let's call this label PAST.
LOD
x ; if x != 0
JMZ ELSE
LOD #2
; y=2 if-true clause
STO y
JMP PAST
; else:
ELSE: LOD #3 ;
y=3 if-false clause
STO y
PAST: LOD #5 ; x=5 past if-else statement
STO x
We are finished, since the if-false part can flow right into the part past the if-else statement. Look again at the jumps and confirm that the right parts of the code are visited whether the condition is true (not 0) or false (0). This code is copied in example ifElse3.asm and described in the video on jumps. Be sure to test it:
Test it by
Note: I use a colon to end a code label in my Pip assembler,
even a name like ELSE.
A label like "ELSE:" can be used more like in Python if you put it on a line of its own just before the instruction to be labeled. This is equivalent to the previous code:
LOD
x ; if x != 0
JMZ ELSE
LOD #2
; y=2 if-true clause
STO y
JMP PAST
; else:
ELSE:
LOD #3 ;
y=3 if-false clause
STO y
PAST:
LOD #5 ; x=5 past if-else statement
STO x
if condition:
block1
else:
block2
linesPastIf
then it can be translated to the general Pip form below. (For
each if-else construction in the same program, you would need different
label names.)
|
Evaluate condition (so false is 0) |
|
|
JMZ ELSE (if the condition is false, skip block1 to the ELSE label) |
|
|
block1 translated |
|
| ... |
|
|
JMP PAST (skipping the else part) |
|
|
ELSE: |
block2 translated |
|
... |
|
|
PAST: |
linesPastIf translated (end up here after either block is executed) |
|
... |
5. Another example to try (with a partner), translating
into an assembler file (ending in
.asm):
if z < 0:
z = z + 10
else:
z = z - 1
z = z * 2
Test your code as in the previous examples.
6. A further example for you to work out by yourself and then
check. Not
only is there just one instruction that checks numerical order, it only
compares to 0, unlike y > x. What do you do? What
comparison to 0 is equivalent? Place different values for x
and y in memory by hand in pipGui.py to test the code:
if y > x:
x = x*2
else:
y = y*2
z = x + y
My code is in ifElse6.asm, if you want to compare at the end.
See the assignment Pip Program. It is similar to the code from this section.
This hopefully gives the idea that a high level language can
be translated. We have kept the Pip simulator very simple, but
with a few more instructions, we could also handle lists and function
calls. We will not take the time to do that in this course.
Aside: Though not a part of the course, the program for the Pip Simulator is a collection of Python modules. They show a considerably larger and more complicated program than anything you have done (over 1000 lines - still much less than the hundreds of thousands of lines of other Python programs). Still most of what is used is basic building blocks that you have learned. There are some Python features used that we did not get to in the Tutorial: I defined two of my own kind of objects; I used list comprehension, exception handling, and some library functions that we did not introduce. You have the source code if you are curious!
We started with machine language and quickly shifted to spend most
of our time on assembler. The progression is an important
idea. To show that you understand the idea of encoding an
instruction as a binary number, you should be able to convert both ways
between machine language and assembler (with a table of the op codes
handy). Both algorithms are fully stated next:
Converting to machine language from assembler:
if the
assembler code contains a '#':
the first 4 bits
are 0001
else:
the first four bits are
0000
The second four bits come from the mnemonic as shown in
this table:
ADD 0000
AND
1000
CPZ 1010
CPL
1011
DIV 0011
HLT
1111
JMP 1100
JMZ
1101
LOD 0100
MUL
0010
NOP 1110
NOT
1001
STO 0101
SUB
0001
if the the mnemonic is HLT or NOT:
the last byte is 00000000
else if the mnemonic is JMP or JMZ:
the last byte is the code address (expressed in binary) to jump to
else if
the assembler contains '#':
the last byte is
the number after '#', converted to binary
else:
the
last byte is the address of the data referred to at the end of the
assembler instruction (in binary)
Converting to assembler
code with numeric labels from machine language:
Split the
machine code into the first four bits, the next four bits, and the
last eight bits.
The second four bits of the machine language
determine the mnemonic:
0000 ADD
0001 SUB
0010 MUL
0011
DIV
0100 LOD
0101 STO
1000 AND
1001 NOT
1010
CPZ
1011 CPL
1100 JMP
1101 JMZ
1110 NOP
1111
HLT
If the instruction is HLT, NOP or NOT:
done!
else:
If the first 4 bits are
0001:
the mnemonic is
followed by '#'
The assembler code ends
with the the last eight bits converted to decimal
Sample conversions to do by hand for understanding. (You can
check your answers with pipGUI.py, switching from showing binary
(Binary button) to showing asembler but no labels (None button).
We have illustrated a simple machine language and
seen how multiple machine language statements can be used to do
central operations in a high level language. This language is
simple, but still it has been described in words! How can a
machine language be expressed in hardware? This section
addresses that question, in stages.
First we consider the
direct correspondence between Boolean expressions, truth tables,
and simple digital circuits. It is useful to be familiar with
all three, since each is more natural or simple in different
situations. It is important to be able to choose the best one and
convert
between them. In particular we can first express
the operations we want logically, and then in
circuits which could be expressed in hardware.
We have already seen Boolean expressions in Python, with operations AND, OR, and NOT. We will end up building more complicated expressions than we did with Python, and more concise notation will be useful and is standard in such discussions. First we will use 1 and 0 for True and False, our usual symbols to distinguish a bit of information. Second we will use more algebraic notation:
A or B is written with a + sign: A + B
A and B is written just by putting the parts beside each other, as with mathematical notation for multiplication: AB (We will assume one character variable names like in math, so this makes sense.)
not A is written: A'
Because there are only a few possible
values for the inputs to the expressions, we can write out a complete
table of possible values, called a truth table. In the
leftmost columns we write the variable values in all possible
combinations, and in one or more further columns write values of
results:
Truth Table for OR 0 only if all inputs are
0
|
A |
B |
A+B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Truth Table for AND 1
only if all inputs are 1
|
A |
B |
AB |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Truth Table for NOT
reversing the input
|
A |
A' |
|
0 |
1 |
|
1 |
0 |
As in Python assume NOT has highest
precedence followed by AND, with OR last.
Another Boolean logic operation
that is occasionally used is XOR, short for eXclusive OR.
It is visually and logically a variation on OR. The
standard OR is true if one or more inputs are true. XOR
is true when exactly one of the two inputs is true, or
otherwise put, when the two operands are unequal. It has
a special operation symbol in Boolean expressions that is also a
variation on the standard symbol for OR. Rather than a plain
'+', it has a circle around it: ⊕
Truth
Table for a Xor 1 when the inputs are unequal
|
A |
B |
A⊕B |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
If I use this less familiar operation in
a larger expression with other binary operations, I will always use
parentheses to indicate the order of operations around the ⊕.
We can calculate truth tables for more complicated expressions, building up one operation at a time. Consider AB'. Since not has higher precedence than and, this is the same as A(B') rather than (AB)'. We need B' calculated before we can calculate AB'.
Truth Table for AB' (involving intermediate result B')
|
A |
B |
B' |
AB' |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
We can have more input variables
involved as in AB + AC. Here we have three input variables, and
2*2*2 = 8 combinations of inputs to list. For consistency, it
is traditional to list the input in the order where they appear as
binary numbers for 0, 1, 2, .... Intermediate results are included in
the table in such a way that each column after the input variables is
the result of one operation on one or two previous column:
Truth Table for AB + AC
|
A |
B |
C |
AB |
AC |
AB+AC |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
Truth Table for A(B + C)
|
A |
B |
C |
B+C |
A(B+C) |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
You can see from the exhaustive listing of the options in the
last two truth tables that AB+AC = A(B+C) always.
This
is called an identity, and it has the same formalism as the
distributive property in normal real number algebra, though
the operations involved are actually completely different!
|
Property name |
AND version |
OR version |
|
Commutative |
AB = BA |
A+B = B + A |
|
Associative |
(AB)C = A(BC) |
(A+B)+C = A+(B+C) |
|
Distributive |
AB+AC = A(B+C) |
A+BC = (A+B)(A+C) |
|
Identity |
1A = A |
0 + A = A |
|
Complement |
(A')' = A |
A + A' = 1 |
|
DeMorgan's Law |
(AB)' = A' + B' |
(A+B)' = A' B' |
Various sorts of switches have been
used historically in computing devices, depending on the technology
of the times: relays (switches actuated by electromagnets), vacuum
tubes, and transistors. All have
the same essential behavior, except transistors are much faster and
more
reliable than the others. I will just refer to the modern
version, transistors.

I will diagram a transistor as a gray circle. A
transistor has three connections, a base, B, an emitter, Vin,
and a collector, Vout.
The base acts as a switch:
If the base is grounded, the emitter is not connected to
the collector. The symbol for ground is shown connected to the
base in the left diagram above. If a voltage is applied to the
base, an
electrical connection is enabled between emitter and
collector.
Hence a transistor has two states, switched on or off.
Circuits are set up with a voltage
source and opportunities for wires to be grounded. The
circuits are set up (with electrical resistances - we will skip
elaborate physics) so if a wire is connected to ground, it is
grounded, whether is is also connected to a voltage source or
not.
Vin is always connected to a
source that might have
a voltage on it or be grounded or be disconnected, while Vout
may either be disconnected or grounded (but it does not have a
voltage attached). The standard ground symbol is shown at the
bottom of each diagram below. A capital V is used to mean a
consistent voltage source. A connection of the output to
voltage or ground is shown by a gray path.

In
the simplest situation, Vin is definitely connected
to a voltage source and also to an output wire. Vout
is grounded. In this case the state of the base is the
only thing variable. As the right diagram shows, if the base has
a voltage, the emitter circuit
is connected, and ground at Vout is connected to the output
through Vin, so the output becomes
grounded. If the base does not have a voltage, as in the left
diagram, the connection
between the output and ground is broken, and the output is just
connected to the regular voltage source, resulting in a voltage on
the output wire.
Possibilities in the Figure
|
Base |
Output |
|
voltage |
grounded |
|
grounded |
voltage |
The circuit provides an output
that is the opposite of the input. If we associate voltage with
1 and grounded with 0, we get the NOT truth table! The NOT
operation takes only a single transistor.
Possibilities
in the Figure
|
B |
Output = B' |
|
1 |
0 |
|
0 |
1 |
We can connect two transistors in
series as shown and use both bases as inputs.

Only
when both inputs have voltage, as shown, is there a connection
between ground and the output. If either input were grounded,
the connection of ground and output would broken, and the output
would hold voltage rather than being drawn to the ground state.
Hence if we call the inputs A and B and the output X, we
get what is called a NAND gate.
Truth Table for a Nand gate:
|
A |
B |
X = (AB)' |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
This the truth table for (AB)', (Python NOT (A AND B) ), and the
combination is commonly abbreviated, NAND.
We can also
connect two transistors in parallel as shown, still using both bases
as inputs feeding one output.

The
only way to avoid a connection between the output and ground is
to have both inputs grounded, as shown above, resulting in
voltage at the output. If at least one input has voltage, the
output becomes connected to ground. Hence if we call the inputs
A and B and the output X, we get what is called a NOR gate:
Truth Table for a Nor gate:
|
A |
B |
X = (A+B)' |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
0 |
This is the truth table for Python NOT (A OR B), commonly
abbreviated as NOR.
To turn a Nor circuit into an Or circuit, a
further NOT operation is needed on the output, requiring one
more transistor. Similarly you can convert a Nand to And with an
extra transistor.
In
circuit diagrams, the details of the combinations of
transistors, voltages and grounds needed for the different Boolean
operations discussed above is hidden, or abstracted away. The
operations are given special, more simple symbols:

The
inputs are assumed to come into the wires on the left and the output
go out from the wire on the right. All the gates that involve
"NOT" have a small circle where the NOT operation would
take place.
For example the Boolean expression A(B+C)
corresponds to the circuit diagram

Each
input is assumed to correspond to a voltage on a labeled wire,
usually coming from the left. These wires feed gates with
result wires coming out of them. As long as each wire ends up
going to the left, and not looping, each wire corresponds directly to
one Boolean
expression. Following the wires, putting the symbolic result
as a label on each one in turn, eventually leads us to an output.
There is a direct correspondence between the intermediate wires (like the one labeled B+C above), their logical labels, and intermediate columns you should put in a truth table when looking to figure out the table for a boolean expression involving multiple operations.
These are sequential circuits. Circuits with loops in them are also important, but more complicated. They are call combinatorial circuits and will be briefly discussed later.
We will mostly work in terms of AND, OR, and NOT, because of
their familiarity, though NAND and NOR are used more in actual
engineering practice, since they require fewer transistors in a
circuit.
By putting more than two transistors in series or
parallel, NAND and NOR gates with more than two inputs can be
constructed, hence with a further transistor for each added input,
multi-input AND and OR
gates can be constructed. The same AND and OR gate symbols are
used in these cases, except more input wires are allowed.
This section was originally developed with an old circuit simulator that is not longer useful. The idea is the same as http://logic.ly/download/. You can get a free 30-day download. It uses about the same symbols, dragging them into position, dragging between terminals to create wires. In the new version there is no button to delete a wire: just click in the middle of the wire and press the delete key. In this version simulation is automatically running. In the newer version there are no intermediate terminals: all wires go from and output terminal to an input terminal. Several wires can start from the same output terminal. Clicking on Help pretty well describes the use of the application. I wish I had this one when I first made the diagrams and videos!
Another option, completely free, is logisim from http://sourceforge.net/projects/circuit/.
Select the download button. The pictures can be fancier, with
labels and there are more settings that you need to make (and hence more to confuse you and more to learn). There
is an intro tutorial.
Watch the gatesApplet video, as I select and move components, connect
them
with
wires, run the circuit and change input values Try similar things
with the logsim simulator. The video ends with a
demonstration discussed in the next paragraph (though using the old
simlator images).
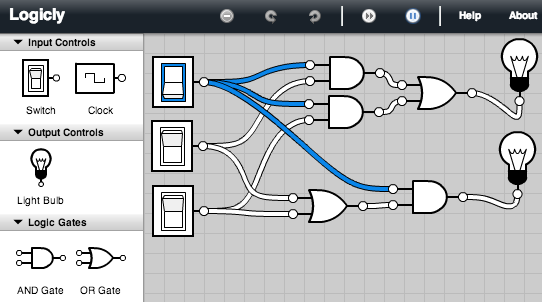
The
following circuit tests the distributive property, AB+AC = A(B+C),
assuming the inputs are labeled down from the top A, B, C. The
circuit has outputs for both sides of the identity originating from the
same inputs, that fork two ways. (This is fine, an input can feed
several
gates.) No matter
how you manipulate the three switches to give all the possible inputs,
the two outputs always match. This is
illustrated for inputs 1, 0, 0 and for 1, 0, 1, where we use 1 to
denote a switch with voltage, denoted in the simulator with a blue
rectangle around the switch. The convention is
that wires only go from the output of a component to the input of
another, with only one wire going to any input terminal.

In the introduction, I mentioned that we want to be able to
convert between all the representations: circuit, boolean expression,
and truth table. We have discussed the
direct translation between Boolean expressions and circuits, and we
have shown how to convert a Boolean expression into a truth table.
The only direction missing now is from truth table to Boolean
expression.
Below is a truth table for an output X. It
is totally specified by the truth table, without first being
given by a Boolean expression. To find a Boolean expression
that does correspond to the output X, first locate a 1 in
the column for X. The final row is an example. This is
true when we have the exact input values in the row: A is true and B
is true and C is true. That is a simple statement to translate
into boolean symbolism: ABC. Another row where X is one
is the third from the bottom, where A is true and B is not
true and C is true. Another way to put this is A is true and
(not B) is true and C is true. Again, this easily translates
into a Boolean expression: AB'C. The chart below traces
out the sequence of steps, including for the second row :
A
B C X Example
0
0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0
0 0
1 0 1 1
1 1 0 0
1 1 1 1 <-
First find an expression producing this 1 and = 0 everywhere else
A
B C X
0 0 0 0
0 0 1
1
0 1 0 0
0 1 1 0
1 0 0 0
1 0
1 1 <- Find
expression producing this 1 and =
0 everywhere else
1 1 0 0
1
1 1 1 ABC
A B C X
0
0 0 0
0 0 1 1 <-
Find expression producing this 1
and = 0 everywhere else
0 1 0 0
0
1 1 0
1 0 0 0
1 0 1 1 AB'C
1 1 0 0
1 1 1 1
ABC
A B C X
0 0 0
0
0 0 1 1 A'B'C
0
1 0 0
0 1 1 0
1 0 0 0
1 0 1
1 AB'C
1 1 0 0
1
1 1 1 ABC
We have expressions = 1 ONLY in
each individual place X is 1. To get X, which is 1 with any of these inputs, combine with
the OR operation:
X
= A'B'C + AB'C + ABC
A circuit could certainly
be made for X, but it would be easier with a simplification. One
advantage of Boolean algebra is that it is easy to manipulate
algebraically, for instance using the rules of Boolean Algebra discussed earlier. I
will not hold you responsible
for this, but it will shorten some answers, and hence prove to be
convenient!
Focus on the last two terms:
A'B'C
+ (AB'C + ABC)
= A'B'C + AC(B'+B) distributive rule
(factoring out A and C
= A'B'C + AC(1) complement
rule for OR
= A'B'C + AC identity
rule
One general rule that is easy to check that was
not in the earlier rules is
A + A = A
In
general, this means any expression can be replaced by two ORed copies
of the same expression. In particular the one copy of AB'C
in the middle of the expression for X can be replaced by two copies
ORed:
X = A'B'C + AB'C
+ ABC
= A'B'C + AB'C +
AB'C + ABC adding a second ORed copy of AB'C
=
(A'B'C + AB'C) + (AB'C + ABC)
associating parts usefully
= (A'B'C +
AB'C) + AC
using
the result above for the last two terms
Just
as we showed AB'C + ABC = AC, we can
rework the first two terms:
(A'B'C + AB'C) + AC
= (A' +
A)B'C + AC
= (1)B'C
+ AC
= B'C + AC
The
general pattern that simplifies is when all but one factor
matches in two terms: then the non matching factor
(negated in one term and not negated in the other) can be completely
removed and leave only one term with the remaining common factors.
Symbolically, if X stands for all the matching factors and Y is
the one non matching factor
then XY + XY' = X.
Find a truth table for the Boolean expression that is true when
all three inputs (A, B, C) are the same (call this X
initially). Then find the Boolean expression in terms of A, B,
and C.
A B C X
0
0 0 ?
0 0 1 ?
0 1 0 ?
0 1 1 ?
1 0
0 ?
1 0 1 ?
1 1 0 ?
1 1 1 ?
Coming up with a completed truth table involves an inital translation from English:
A
B C X
0 0 0 1
0 0 1
0
0 1 0 0
0 1 1 0
1 0 0 0
1 0
1 0
1 1 0 0
1 1 1 1
Now
what to get a Boolean expression?
A B C X
0
0 0 1 <- First find AN expression matching this 1
and = 0 everywhere else
0
0 1 0
0 1 0 0
0 1 1 0
1 0 0
0
1 0 1 0
1 1 0 0
1 1 1 1
A
B C X
0 0 0 1 A'B'C'
0
0 1 0
0 1 0 0
0 1 1 0
1 0 0
0
1 0 1 0
1 1 0 0
1 1 1 1 <-
Then find AN expression matching this 1 and = 0 everywhere else
A
B C X
0 0 0 1 A'B'C'
0
0 1 0
0 1 0 0
0 1 1 0
1 0 0
0
1 0 1 0
1 1 0 0
1 1 1 1 ABC
Then
what?
Combine with OR:
X = A'B'C' + ABC
A common student error is to skip the last step, and not combine,
but you are looking for a description of a single output, so your
result must be a single expression!
OK so we can
convert logical operations to hardware. In all our logical
operations, however, we did not see normal
arithmetic, but we want to be able to do that on a computer!
Since
we are using two state circuits we will do binary arithmetic.
Start
as simply as possible. If we stick to 1 bit additions, there
are not many choices:
0 0 1 1
+0
+1 +0 +1
__ __ __ __
0
1 1 10
The complication is the carry in
the last case. It means we need to keep track of two binary
outputs which we will call sum (the 1's bit) and carry (the
carry bit). All the data is 0's and 1's, so we can write a
complete table:
Table for sum and carry in
binary addition, A+ B
|
A |
B |
carry |
sum |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
We are thinking of arithmetic, but see the format of the table - it
is in the format of a truth table!
You may recognize both the outputs: carry
is AND and sum is XOR.
If you wish to avoid the XOR
symbolism, you can calculate an equivalent expression in terms of
AND, OR, and NOT, as we can for a truth table. Applying the
technique just introduced for finding a Boolean expression from a
truth table, you find:
A XOR B = AB' + A'B
This is a half adder circuit.

The video animates this circuit. If you like you can construct
and test the circuit for yourself in the gates applet,
To
understand more complicated circuits it is useful to give a simpler
symbol for repeatedly used circuits. We will use the half adder
several times in more complicated situations, and will give the half
adder its own symbol

When
you do addition using place value with two multi-digit numbers,
you actually have to add three digits together at a time in general:
a digit from each number, and a possible carry
from the previous place. An example as you might have written
it in primary school to add 5147 and 7689:
1 11 carries
5147 decimal numeral
+ 7689 decimal numeral
_____
= 12836
If
you are adding multi bit binary numerals, that means adding three
inputs that can be 0 or 1, with a sum at most 3, still only needing 2
bits of output.
111 carries
011 binary numeral
+ 111 binary
numeral
_____
= 1010
We can put two half adders together with one extra OR gate to
create a full adder, which
adds three single bit inputs, as
illustrated below in terms of the just-introduced half adder
symbol. If we label the three inputs A, B, and "carry in",
then we can start adding A and B with a half adder. The sum
output can be added to the carry in with another half adder to
produce the final sum bit. Both half adders have a carry bit.
If either one produces a carry, then there is a carry in the
final answer, so the carry bits need to go through an OR gate to
procuce the final carry.

Recreating this in the gates applet is shown in the video, and also
below in pictures. The most significant output bit
(carry) in at the bottom. You could also create your own and test
it in
the gates applet, but the circuits are getting more complicated to
reproduce by hand!
. 1+1+1 =11
1+1+1 =11
 1+0+1=10
1+0+1=10
The full adder,
too, can be used in more complicated circuits, so we will give it its
own symbol:

Once
you have full adders you can chain them together to create a
multi-bit adder. For example, a circuit to add two three-bit
numbers could get inputs A2, A1, A0,
and B2, B1, B0, where the subscripts
indicate the power to which 2 is raised in the binary place
value. The result produces three sum bits for 2 raised to
powers 0, 1, and 2, and a further bit for the final carry
(representing 23). The addition in the lowest order bit
has no carry in, so only a
half adder is needed:

Recreating this in the gates applet is shown below in pictures, and is
simulated in action in the video. For
example, consider these two calculations:
11
011
010
+101 +101
____ ____
1000 111
The pictures below show these two calculations in a circuit, with
the more significant bits in both the input and output are lower down
in the diagram. The top summands in the manual calculations above
correspond tothe leftmost column of switches, and the bottom summmands
reappear slightly to the right.
 011+101=1000
011+101=1000
 010+101 = 111
010+101 = 111
A
multiplexer chooses one of several data
lines. In an n-bit multiplexer input consists of 2n
data lines and
n
control lines for some positive value of n. There is one output
line. The n control lines have 2n
possible states and hence they can be wired to determine which of 2ndata
lines should go to the one output line. For example if the
control lines hold a memory address, multiplexers can be used to fetch
the data from the proper source. For a dynamic illustration, see
the video N5G.
The simplest version to illustrate is a 1-bit multiplexer shown
below. It shows 2 data line and 1 control line (the
control line can choose between two states). In the pictures
below data bits are indexed by 0 at the top, 1 below, and the one
control
line at the bottom chooses between them. For example, in
the first picture the control
line is off (0), so the input with index 0 (the upper one) has its
state (on, 1) transmitted through to the output wire, lighting the
light.
 d0=1, d1=0,
control choosing d0 = 1
d0=1, d1=0,
control choosing d0 = 1
 d0=1, d1=0,
control choosing d1 = 0
d0=1, d1=0,
control choosing d1 = 0
 d0=0, d1=0,
control choosing d1
d0=0, d1=0,
control choosing d1
The pictures below, and also the Multipler video show a 2-bit
mutiplexer, with 4 data lines and 2 control lines. (Do you see
that it is
composed of three of the simpler multiplexers?) In general
there could be 2n data lines and n control
lines. The data lines in the picture are numbered 00 through 11
from top to
bottom. The top control line has the less significant bit.
 d00=0,
d01=0, d10=0, d11=1, control choosing d01 = 0
d00=0,
d01=0, d10=0, d11=1, control choosing d01 = 0
 d00=0,
d01=1, d10=0, d11=0, control choosing d01 = 1
d00=0,
d01=1, d10=0, d11=0, control choosing d01 = 1
 d00=0,
d01=1, d10=0, d11=0, control choosing d11 = 0
d00=0,
d01=1, d10=0, d11=0, control choosing d11 = 0A
demultiplexer does the reverse: n control lines and one data
input line deliver the input value to one of 2n output
data lines.
Multiplexers are needed to fetch data from one of
many memory addresses. Instructions must be fetched, using the IP
address to feed the control lines. We need to get data into a
register, like the accumulator in Pip, using the address byte in an
instruction to feed the control lines.
Also Demultiplexers are needed for the reverse: getting data
from the accumulator to one of many memory addresses.
Multiplexers
can also be used inside a CPU to get the result from a specified
operation code: The computer actually works out all possible
operations at the same time, feeding data lines into a
multiplexer; the op code feeds the control lines of this
multiplexer to pick the result
associated with the right op code.
We have only
considered sequential circuits - signals flow through and nothing is
kept. We need a combinatorial circuit, one with a loop in it,
to have memory. Loops in circuits can get tricky.
A latch can
remember a value. We examine it in steps.

It
has two main direct inputs d, the data
value, and g, which is 1 as we shall
see when the circuit should get
the data. Note the two lines
feeding back from the nand outputs y and
z.
Also z flows to the final circuit
output q.
The three nand gates correspond to Boolean relationships x = (dg)'; z =
(xy)'; y = (g'z)'
If g
is 1, then g' is 0, and this simplifies
to x = (d1)' = d'; y = (0z)' = (0)' = 1,
so z = (d'1)' = (d')' = d, and q
= z: that means the value of d
is transmitted to the output, whatever d
is, and however it changes over time.

On the other hand, if
g is 0, then g'
is 1, and it is more complicated, and we must take the old value of z
into account: call that old value q,
so q = z. Then x
= (0d)' = 1, and d has no
further effect. y = (1q)' = q'
which then circles around to make z = (1q')' =
q, which is what it was before, so the loop maintains its
old value of z (and
also its value of y similarly),
independent of how d is changed!

It
is not quite that simple if you view the latch video. If you try
to
recreate it and run it in a simulator with lower input g = 1, you can
switch the upper input d and have it behave as expected. However
if you change d to 1 and then change g to 0, then depending on your
Java implementation for the applet, you could see the
circuit flash continuously, back and forth between the two pictures
below:


That transition
of g from 1
to 0 is a problem. This is a timing
issue. See the slight
alteration below. See that two extra NOT gates are inserted.
In
a static logical state they cancel each other out, but they change
the timing when the signal from g alters and splits. Now
runing a simulation works, if you start from a stable state, with any
sequence of input data, and it should
work (hopefully in whatever circuit simiulator your browser is
using).
 With g=1, data
1 passes though. If data were switched to 0, output would go to 0.
With g=1, data
1 passes though. If data were switched to 0, output would go to 0.
 g to 0, keep output 1
g to 0, keep output 1
 g at 0, data switched to 0, but output still 1
g at 0, data switched to 0, but output still 1
 g to 1,
output matched data, 0
g to 1,
output matched data, 0
When the lower input (g) is 1, the output changes with
the upper input (d). When g is changed to 0, the last output is
remembered, no matter what you do later to d.
This
example indicates the importance of timing. We have left out a
discussion of the regular alternating clock signal that is used to
synchronize and stabilize outputs. A deeper examination of
circuits would include a clock.
See
the gates homework.

For much more detail (going far beyond this course!), see VLSI.
So we have gotten as far down to basics as we are going to in this
class. (Below
this is chemistry and physics!) We have described some of the
most important hardware used in creating a computer, seen how
millions of components can be put together efficiently to create a
machine with
its machine language, and some of the major points in the translation
between machine language and a high level language.
There is much more to study. Here are a few examples:
Comp 264, Computer Systems, covers
what lies under high level languages in much greater depth.
A sequence of programming courses, starting with Comp 170, show ideas needed for more sophisticated programs to solve much larger problems.
There are a great many topics in computer science beyond programming, addressed in upper level courses:
networking and security,
devising algorithms for handling
all kinds of enormous collections of data,
getting many processors and many computers to work together effectively on enormous problems,
dealing with the many legal and ethical issues around computing,
approximating human intelligence (so far only in specialized ways),
and finally finding the limits of computing - it cannot solve all problems.
There is much more to learn and apply to the pressing problems of today and tomorrow! We live in the information age! Will you be a leader in it?
We have been dealing with the current practical model, with Boolean electical components on a chip. Completely different approaches are being researched and may have practical application in the future: optical computers, quantum computers, DNA computers, ....