Detailed outline of past class accomplishments and future plans
Class 1
Groundrules, Admin
FiniteFields.pdf: primes, divisors, gcd
extended gcd: xgcd.pdf
Python
intro: PythonBasics.pdf
+ my CommentsOnPythonBasics.html
Alternate view - compare with Java
JavaVsPython.html
develop code for Euclidean algorithm - loop and recursive
uploaded something close to the result: gcd.py
see code for extended Euclidean: xgcd.py
HW includes extended gcd, recursive
Class 2:
Python start:
See JavaVsPython.html for added parts as needed on multiline
statements, assert,
function
signatures,
string
formatting, dictionaries/maps,
first
class objects, and using classes.
List comprehensions, Doctests
recursiveTuples2.py for doctest
develop power functions: slow, fast
time analysis of both methods in terms of power n (For now assume
each multiplication takes same time. When done mod m, as will usually be the case, this is true.)
Order estimates: see parts of
http://en.wikipedia.org/wiki/Big_Oh
Bases.html
bases.py for practice with lists, loops, essential base idea!
Develop arithmetic time analysis
simplistic gcd time analysis: if k bits: O(k3)
ri = qiri-1 + ri-2 >= 2* ri-2
so the remainders shrink exponentially, and the number of steps is
bounded by O(log a) which is O(k). All individual
operations are O(k2), based on a maximum of k bits, giving the easy total O(k3).
Fancier book analysis base on the fact the the product of all the
quotients is less than a, shows the extended Euclidean angorithm takes
O(size(a)*size(b))
Actual computers do 32 or 64 or 128 bits at a time, but the same order results.
Back to FiniteFields.pdf: group, rings, fields See the ErrorInFiniteFields
There is Hw from the end of FiniteFields.pdf: 2, 4, 5ab, 6, 8
Python:
Defining classes: Silly simple example animalW.py,
coding infix operators for groups and fields:
simple version for a concrete group mod26A.py,
More robust version allowing operations with integers, too mod26.py,
Class 3
Finish mod26.py. Generalization to arbitrary modulus, with code for fields mod_arith1.py.
HW: improve naive inverse() and __pow__ methods.
Multiplicative subgroups
Z/nZ*, the invertable elements of Z/nZ, is a group under multiplication, called the multiplicative group of Z/nZ
Z/nZ*
is group, because it is closed: (ab)-1 = a-1 b-1. The number of elements in Z/nZ* is defined as 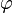 (n), the Euler phi function or Euler's totient function.
(n), the Euler phi function or Euler's totient function.
For prime p, Z/pZ* contains all elements of
Z/pZ except 0, and hence Z/pZ is a field. I like the (shorter) notation for Z/pZ, emphasizing that it is a field: Fp
The Euler phi function will be very important for cryptography:
If p is prime, what is 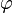 (p)?
(p)? 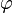 (pk)?
(pk)?
More on phi:
http://en.wikipedia.org/wiki/Euler_phi_function
Fermat's Little theorem is the basis of RSA:
http://en.wikipedia.org/wiki/Proofs_of_Fermat%27s_little_theorem
Group theory proof
http://en.wikipedia.org/wiki/Proofs_of_Fermat%27s_little_theorem#Proof_using_group_theory
which in turn uses Lagrange's theorem
http://en.wikipedia.org/wiki/Lagrange%27s_theorem_(group_theory)
To calculate the phi function easily we can use the Chinese Remainder Theorem
http://en.wikipedia.org/wiki/Chinese_remainder_theorem
The page constructs a solution, but does not include a proof that it is unique.
If x and y are solutions, then z = x-y solves z mod ni = 0, i = i, 2, ...k,
Hence z is a multiple of each ni. Since the prime factors of the ni are disjoint, z is also a multiple of N, and x = y mod N.
Now to help calculating phi:
Alternate proof that
Phi is multiplicative:
For coprime m,n, 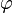 (m)
(m)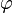 (n) =
(n) = 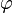 (mn)
(mn)
Proof: We have a correspondence between (a,b) in Z/mZ X Z/nZ and
x in Z/mnZ via the Chinese Remainder Theorem, but we only want to deal
with the multiplicative subgroups.We have not show the direct correspondence between them, but we can:
Assume the setup for the Chinese Remainder Theorm, with two equations:
x mod m = a, x mod n = b.
assuming gcd(m, n) = 1.
We get the correct count if the following is true:
if gcd(m,a)=1 and gcd(b,n)=1 iff gcd(x, mn)=1.
Proof =>
In this directon we can add the assumption
gcd(a,m) = 1 gcd(b, n) = 1.
Since gcd(m,n)=1, there are s and t so
sm +tn = 1.
This also means gcd(m, t) = 1.
x = bsm + atn is the construction in the Chinese Remainder Theorem.
The
assumptions above say none of the factors a, t, n in atn has a common
factor with m, but of couse bsm has m as a factor, so x = bsm+atn
shares no common factors with m.
By a symmetric argument, x shares no factors with n.
Hence x shares no factors with mn, and gcd(x, mn) = 1
Proof <=
Conversely, if a and m share a factor, so do x and a, since x = bsm + atn.
The argument for b and n is symmetric.
Done.
In particular, we will use the fact for RSA that for distinct primes p,q: 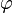 (pq) = (p-1)(q-1)
(pq) = (p-1)(q-1)
Class 4
Questons on Cryptography intro?
Do examples
Caesar
See caesar.py
...
Matrix operations and inverses are mentioned in several places, but not anything about algorithms
Based on solving systems of linear equations. What are approaches?
Basic examples, oprations, solutions, translations
http://en.wikipedia.org/wiki/Square_matrix
There are many more sub-topics than we need! We will focus on the
relationship between matrices and systems of linear equations,
determinants, theoretical definition and efficient calculation with
systems of linear equations. Issues associated with different
number systems as elements: floating point, integer, modular
group, modular field, special case of mod a power of 2. Rings of matrices.
http://en.wikipedia.org/wiki/Determinant
See the intro, sections 5 - 8.1
http://en.wikipedia.org/wiki/Elementary_row_operations
See http://en.wikipedia.org/wiki/Gauss%E2%80%93Jordan_elimination
Eventually look at gaussJordan2.py uses mod_arith (solution to HW3) - in the form mod_arith.pyc online
The original Gauss-Jordan algorithm depends on having inverses on each
row, though the theoretical derivation through determinants only needs
an invertible determinant. For instance in the mod 6 matrix
3 2
2 3
all the elements are zero divisors, but its determinant is 3*3 - 2*2 =
5 = -1, invertible. In fact the matrix is its own inverse!
We can get there with elementary row operations, NOT multiplying by a 1 divisor:
3 2 1 0
2 3 0 1
r1 <- r1 - r2
1 -1 1 -1
2 3 0 1
r2 <- r2 - 2*r1 (using 5 = -1, 3 = -3)
1 -1 1 -1
0 -1 -2 3
r2 <- -r2 (-3 = 3)
1 -1 1 -1
0 1 2 3
r1 <- r1 + r2
1 0 3 2
0 1 2 3
so the matrix is shown to be its own inverse by row operations that do not multiply the determinant by a zero divisor.
OK, that is a concrete example. In general if a and b are
in the current column worked on, and a = qb + r (integer arithmetic),
then you can replace the row with the a so the column entry
becomes a-qb = r, and you could continue working with this row and the
row with the b, following the sequence of operations for the gcd until one row
contains gcd(a, b), all with row operations that do not change the
determinant.
In the example above, after only one step, the gcd was 1, definitely
invertible, but in more complicated cases the gcd for two column
entries may not be 1 and it may even be a 0 divisor. You need to
think about that carefully to attempt HW4 problem E, and prove the
algorithm works in general.
For extra extra credit in 331 (or extra credit in 431) you can avoid an
extra level of looping if you look at the multiples coming from the q's
and see how they relate to xgcd. Try an example. This does
not go quite far enough by itself, See the slight elaboration of xgcd,
mgcd with its documentation string, in the revised xgcd.py. It could speed up the algorithm....
Class 5
More determinants:
Relation of determinant of
1 2 3
2 5 9 to
4 0 1
2 4 6 5 2 3 2 5 9 1 2 3
2 5 9 10 5 9 1 2 3 1 2 3
4 0 1 20 0 1 4 0 1 4 0 1
r1*2
c1*5
r1<->r2 r2=r1
Elaborated gaussJordan2.py:
mxvSolve(m, v, gjSolver) solves mx = v, m a square matrix
transpose(m)
add(m1, m2) m1+m2
sub(m1, m2) m1-m2
linComb(m1, m2, a, b) a*m1 + b*m2
mul(m1, m2) converts plain liat s m1 to matrix [m1]
alternate name convertMat for matConvert (to be conistent wih other names)
elaborated display methods
How was the reading? Questions?
Buchamnn block cypher coding basics capLetCode.py
After class added affineEncrypt function - useful for HW
Posted gaussJordan26.pyc and gaussJorday27.pyc to help with HW (Take the one you need and remove digits from the name.)
Corrected class cryptanalysis of affine cipher: affineCrypt.txt. Thi is an (edited) history of messing in the Python shell - it is not executabel Python.
One trick was to solve AW=C for A, we need to consider the equivalent WtAt = Ct, in order to solve with my mxvSolve, since I assume the unknown matrix is the right part of a product.
Skipping the chapter on the practical AES: important block
cipher, but no real intellectual content. It is just a recipe
that is quick to execute in hardware. It does get used for a
sequence of blocks, and the sequential block algorithms from your
reading are important
there. By the way, in Python bitwise exclusive-or is ^. The
main mathematical content of the block sequence algorithms is just that
(a ^ b) ^ b = a, so f(x) = x ^ b is its own inverse.
Both the block sequence code and AES in Python are in aes.py. You are NOT responsible for AES, beyond knowin it is a secure, fast symmetric block cipher.
The code there for the block sequencing CBC, ... may be clearer to programmers than Buchmann's outline.
On to math and some cryptanalysis of RSA:
http://en.wikipedia.org/wiki/RSA
A small e is breakable. e = 216 + 1 = 65537 is recommended if sent to ONE recipient, but random padding
Class 6
Dr. Doty on finding primes: Fermat's test based on Fermat's
Little Theorem, Carmichael numbers, Miller-Rabin. Follow Ch 7
closely.
Python. I do not know what was wrong with his Python environment
that the Fermat test did not work. I have two versions online in
the code:
FermatPrime.py uses our Mod calculating, which does the powers by squaring, using aclass generated with ZMod.
FermatPrimeDoty.py and the imported modpower.py that he gave you.
There is one strange thing about the terminology. If a<n and a is not
prime to n, then the test of Theorem 7.4.1 will fail, So
the test fails if a is a witness or if gcd(a, n) > 1. Both
indicate n is composite!
I agree with the basic idea of his homework. See my version of the homework, due Monday, Oct 19:
Class 7
error in gaussJordan.showInverse, fixed in latest 2.6, 2.7 pyc files.
Fixed docs for gcd, xgcd
Exam context: MidTermTopics.html
Questions?
gcd(a[1], a[2], ... a[n])
Historical note on primalty testing: Miller-Rabin is an efficient
curent probababalistic test, but it was not the first. For RSA to
be practical, a test is needed. An older test is the
Solovay-Strassen primality test
http://en.wikipedia.org/wiki/Solovay%E2%80%93Strassen_primality_test
which uses Jacobi symbols in a test that reduced the probability of n being composite by only 1/2 each time.
factorAttack.pdf
http://en.wikipedia.org/wiki/Optimal_Asymmetric_Encryption_Padding
or different e values is needed if a message is going to multiple recipients.
RSA.py In real life RSA is not used to directly encode messages!
More math:
Polynomial Fields
The gcd of polynomials will always be taken to be monic.
To extend Fp to Fq where q = pr, you
need an irreducible polynomial of degree r. About 1/r of the
polynomials of degree r are ireducible. For small q you can check
a random polynomial to see if it is irreducible by brute
force. For large q (practical size), you need a more efficient
test for irreducibility. There are fancier tests, but an easy one
to state is
Rabin's Irreduibility Test(1980):
A polynomial f of degree r over the field Fp is irreducible if and only if xq = x mod f, where q = pr, and
gcd(f, xs - x) is a 0-degree polynominal for each s = pr/t where t is a prime factor r.
For example, if r is prime, the requirement is just that xq = x mod f and gcd(f, xp - x) is a 0-degree polynomial.
Class 8 - Midterm
Class 9
Play with polynomial rings and fields, but hand and using
class PolyMod in polymod.py, polynomials over modular rings
class PolyModP in polymodp.py, for finite fields of size pr: polynomials over Z/pZ mod an r degree polynomial P(x).
Look at
xgcd - updated to use divmod in code and after class do mgcd documentation right!
mod_arith.py - updated so class, not just self provides modulus
projects: finding irreducible polynomials with different levels of efficiency, order of sample elements.
Accumulating a list of irreducible polynomials makes sense, but for any
irreducible polynomial p, k*p is also irreducible if k is a number not
equivalent to 0. It is not useful to inlude all of these, so we
will generally consider monic irreducible polynomials, and use monic
polynomials for polynomial moduli.
A loose end from class: generating a constant other than 0 or 1 in xgcd with polynomials. The little script testpolyxgcd.py produces an example:
xgcd param, mod 7: 5x^2 + 3x + 4 and x^3 + x + 1
gcd: 4 with coefficients: 4x + 6 and 1
so gcd is not 1, but another nonzero constant.
This shows the need for the two-step inversion in PolyModP's inverse method.
Class 10
p-1 attack for RSA code
ElGamal: ElGamal was introducted for a general finite field, with a power of a
prime elements. It works fine if the power is 1, and the manipulations are slightly easier.
An issue for any discrete log approach is finding a generator with a
large order. Recall Lagrange's theorem that the order of each
element divides the order of the group. For Z/pZ*. the order of
the multiplicative group is p-1, and while p is prime, there is nothing
in general we can say about the factorization of p-1 (other than it has
a factor of 2!). On the other hand where we get to choose p, we
can make requirements on p-1 also. As Buchmann suggest we can
look for a prime p so that p-1 = 2q, for another prime q.
How many generators will the multiplitive group have? How can we
easily test the order of a random element?
Later see ElGamalIntHW.py. Homework will be to complete ElGamal cryptosystem in Z/pZ.
Some discrete log attacks (Buchmann Ch 10)
Shanks baby/giant step
http://en.wikipedia.org/wiki/Baby-step_giant-step
start Python code. Finsh for HW
Pohlig-Hellman ruduces work in discrete log when the order of the
multiplicative group can be factored. Start wih multiple primes
in factorization in class. Then case with a power of a prime:
PohligHellman mod pr to mod p pdf
Code PohligHellman.py
Hashing: pdf SHA-1 Python
Notes after class that will discuss more next week:
- I combined and extended the basic factoring/prime functions into factoring.py.
- primeList is copied in from primeSieve.py (no need for primeSieve.py now)
- I included the algorithm I used in carmichael.py to factor using a prime list into factorGivenPrimes
- Since having prime multiplicities is useful not only in PohligHellman, I added factorMultiplicity.
- I modularized PohligHellman.py and renamed things looking ahead:
- Looking
ahead I renamed the special versons that we discussed mod p with,
PohligHellmanModP, getXModP. There are now stubs for future more
general versions where alpha and beta are just group elements, in an arbitrary finite group.
- Rather than mimicing a previous factoring function (bad
programming practice!), I use it (motivating the changes above to
factoring.py)
- I emphasized the brute force discrete log by pulling it into a
function discreteLogModP (and speeded it up). Illustrating a change to
the more general group form, I also added discreteLog for use with an arbitrary group (unused at
present).
- I put Dr. Doty's version of the Chinese Remainder Theorem into my crt.py, keeping his name ChineseRemainder.
- In getXModP:
- I got rid of an extraneous modulus calculation (xFinal < q**r always without the mod q**r).
- I got rid of some of the repeated exponentiation
by introducing qPow,the current power of q, and oDiv, the curent order:
the original group order p-1 divided by the next power of q.
- I got rid of repeated use of xgcd for an inverse, calculating the inverse of alpha, alphaInv, just once before the loop.
- Overall
files to download/update: factoring.py, crt.py,
PohligHellman.py. For reference, I renamed toversion discussed in
class: PohligHellmanOld.py.
Class 11
commnt on generated and PolyMod
Pohlig-Hellman generalize from mod p group, see discreteLogModP vs discreteLog
Rabin irreducible example. PLAN
Comments on HW8 2 -> HW10
More on solving DL: There are other more complicated
methods to describe and prove: Pollard rho; index calculus,
analogous to attacks for RSA. It may be that the (still unknown
possible) killer RSA attack will not translate to the finite fields,
but it may well. We will need to go further afield (or a-group)
to get to very different situations.
ch 12 through 12.6
http://en.wikipedia.org/wiki/Digital_signature
http://en.wikipedia.org/wiki/Universal_forgery
http://en.wikipedia.org/wiki/Digital_Signature_Algorithm
Alternate groups for DL use elliptic curves:
http://en.wikipedia.org/wiki/Elliptic_curve
Class 12
Online code changes: All dirctories under http://anh.cs.luc.edu/331 :
All of what was in code is now copied into code/OldCode for reference.
All that is new is in code/codeChanged and also in codeChange.zip. The overall current update,
with changed code and the code that needed no changes is in usual
directory I link to: code.
I refactored the Mod class. I suggest you copy all your present
code to an oldCode directory, as I have done online, though the changes should not interfere
except in one situation in doctests where they produce "ZMod" in their
output. After backing up, copy all the files in codeChange.zip
over the directory with the current files you have from me.
Changes:
Mod is now a named class in mod.py (shortened from mod_arith.py). You can still you ZMod, as in Mod7 = ZMod(7).
You can now iterate over whole Mod, ModPolyP and Elliptic groups given one element, elt:
for z in elt.group():
....
I added this principally to allow brute force calculations of arbitrary
small Elliptic groups. See findE.py, an interactive place to
print out whole elliptic groups.
There was a bunch of refactoring under the hood, that make the code in
Mod, ModPoly, ModPolyP and Elliptic easier, but is presumably just used
inside these classes. You can skip the rest of this technical
paragraph if you like. The group iterator is implemented uniformly by
calling a new method next in each class, that
produces a next element after self. In Mod and PolyModP this in
turn is
implemented usng the idea in irred.py, encoding each element as an int
with k = int(elt), and reversing this, given a element, other, in the same
group , with other.likeFromInt(k). Cyclic traversal is
possible because of the method totCodes: The sequence of all int
codes for the finite Mod or PolyModP group containing elt are
range(elt.totCodes()). Some common features in my classes are
abstracted out into superclasses defined at the top of mod.py:
FiniteGroup defines methods next and group, and ParamClass defines
methods like and tryLike.
My code: elliptic.py Play with findE.py.
http://en.wikipedia.org/wiki/Elliptic_curve_cryptography
We are not likely to get to it, but elliptic curses also provide an algorithm for factoring!
Elliptic curves for digital signature standard:
http://en.wikipedia.org/wiki/Elliptic_Curve_DSA
Proof is not inthe elliptic variation - but almost line for line
analogous, with some different names, and swapping the symbolism for
the group operation from * to +. I use capital letters for group
elements, G, the generator, and Q, the public key.
k = s-1 (z +rd) mod n
= (wz + wrd) mod n
u1G + u2Q = wzG + wrQ = wzG + wzdG = (wz+ wrd)G = kG = (x1, y1) -> r = x1 mod n
Note: there is no arithmetic relationship between n and the size
of the underlying finite field, and the underlying field could be
formed of polynomials. Hence the conversion to integers of Fq
elements used for elliptic curve coordinates must be agreed on -
presumably the usual canonical integer representation (obtained in my
code by int(x)).
So we have a cryptographic use of elliptic curves. What don't we have that might seem obvious?
How invertibly map a message encoding to an elliptic curve point?
Secret Sharing
http://en.wikipedia.org/wiki/Shamir%27s_Secret_Sharing
HW: SecretShareEncrypt(c, p, n, k) with plaintext c mod prime
p, for secret sharing needing n people to decrypt, k >= n, returning
a list of k pairs (v, f(v)) for an polynomial f of degree at most n-1
over
Z/pZ, that has all coefficients but the constant random, and the
constant = c. (The initial post here was wrong in insisting that
the polynomial be exactly of degree n-1.)
SecretShareDecrypt(pairs) takes n or more of the
secret pairs and returns c. Note: We have only used
polynomials so far as expressions that are elements of a ring or
field. In PolyMod, they are also functions that you can
evaluate: For polynomial p, p(k) gives the value, as a normal
function.
Class 13
Code Updates:
- findE.py: I do the
checks for prime/irreducible input. I assume irred.py exists. You
can change it to irredHW if you need to.
- PolyMod: sparse polynomial constructor and __pow__ with optional polynomial modulus, allowing use of 3-parameter pow function.
- PolyModP: uses PolyMod 3-parameter pow.
I learned something about Python. I did not realize that
__pow__ could be used to define 3-parameter function pow for a new
class unitl I experimented. The last two changes came from that
and the desire to more efficiently deal with powers such as in rabin.py.
Play with gnupg?
Also use for ssh into Loyola
http://syshandbook.cs.luc.edu/how-to/secure-shell-ssh
Public Key Infrastructure
Buchmann 299-306
ftp://ftp.pgpi.org/pub/pgp/7.0/docs/english/IntroToCrypto.pdf
p6 good reference list, technical and poltics
p13 recognize most fo the names?
p18 nice diagram of hash and digital signature
p22 certificate data. NOte we hae not concentrated on symmetric systems - some new algorithm names
p25 Web browsers largest users of X.509 certificates
p27 trust models
p29 complicated PGP model, with marginal trust.... ? 2 marginally trusted = 1 really trusted?
p32 key splitting - we wre more technical with latest hw
p41 The advertisement had to come in here somewhere.
gpg howto:
http://www.dewinter.com/gnupg_howto/english/GPGMiniHowto.html
have a keysigning party!
http://www.cryptnet.net/fdp/crypto/keysigning_party/en/keysigning_party.html
The shell history or me using this is at gpgShell.txt.
odds and ends to fill in:
2.14 element orders. Thm 2.14.1 hw ex?
4.3 birthday (why avoiding hash collisions is hard) Ex 4.8.6
http://en.wikipedia.org/wiki/Birthday_problem
4.4 perfect secrecy, vernam one-time pad
http://en.wikipedia.org/wiki/One-time_pad
8.5 Diffe-Hellman key exchange code?
http://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange
12.8 blind signature
http://en.wikipedia.org/wiki/Blind_signature
14.3.3 zero knowledge proofs: general:
http://en.wikipedia.org/wiki/Zero-knowledge_proof
modular arith based: Code?
http://en.wikipedia.org/wiki/Feige-Fiat-Shamir_Identification_Scheme
Final Review Class
Remember the course surveys: mine (informative for me and next cryptography prof, much appreciated); university's (required for me to pass out)
Go over review with review problems.
Do simpler zero-knowledge algorithm Fiat-Shamir Last week's extra
complicated to get basic idea across; book's poorly written; try:
http://www.cse.scu.edu/~tschwarz/coen350/zkp.html
Since r is random and cannot be recovered from r2, knowing rs does not help determine s, but easy to check (rs)2 = r2s2
Of course getting r donesn't help at all with s, but forces truthful r2. I wil make up a simple example to reinforce this.
Questions? Topics for review?
TAKEHOME EXAM as described in email.
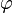 (n), the Euler phi function or Euler's totient function.
(n), the Euler phi function or Euler's totient function. 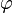 (p)?
(p)? 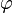 (pk)?
(pk)?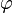 (m)
(m)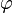 (n) =
(n) = 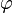 (mn)
(mn)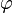 (pq) = (p-1)(q-1)
(pq) = (p-1)(q-1)